鋼結構技術論文
中國建筑金屬結構協會
建筑鋼結構分會主辦
摘 要：北京奧運會大興排練場大跨度交叉威亞主鋼索網是奧運會、殘奧會開閉幕式上空演員、道具訓練的承載基礎，其受力性能對上空設備的安全至關重要。采用理論分析和數值計算相結合的方法，運用ANSYS和EASY程序，對奧運會排練場上空鋼索網的受力特性進行了分析。結果表明，南北單索的最大內力值115.54kN。交叉鋼索網是一個內力重新分配能力很強的自適用體系，最大拉力90.63kN。大跨度交叉鋼索網結構受力合理，安全可靠。
關鍵詞：威亞鋼索網；找形；非線性分析；有限元；力密度法
北京奧運會大興排練場是為解決奧運會、殘奧會開閉幕式演員、道具的排練和威亞系統考核、調試建造的。排練場建有模擬國家體育場內環高度的鋼桁架柱，并在其上建有一個大跨度交叉鋼索網，用來承載威亞，模擬訓練四個儀式空中演員、道具的演練。因此，上空鋼索網體系的受力性能對于演員和設備的安全至關重要。本文對奧運會排練場上空交叉鋼索網的受力特性進行了計算和分析，為設計提供依據。
1 索網體系及受力特點
1.1 索網體系
奧運會排練場上空鋼索布置如圖1所示，是一個由多根放射狀索和鋼管組成的索網體系，共有18根承載鋼索。南北向2根通長承載鋼索，南北向不通長鋼索2根，跨度184m；東西向不通長鋼索14根，跨度126m。東西向和南北向16根不通長鋼索通過空中一根長13.4m的鋼管連接起來，呈放射狀布置。鋼索上設置了荷載為500kg、200kg、100kg三種威亞裝置，用于開閉幕式上空演員、道具排練。這種形式的鋼索網空間結構在國內外尚屬首例。
上空鋼索參數如下：鋼絲繩為6×19S+IWR，公稱直徑32mm，表面鋼絲直徑≥1.5mm，重量4.15kg/m，公稱抗拉強度1870MPa，鋼絲繩最小破斷力632kN。彈性模量6.86×1010Pa，泊松比0.30。中心鋼管直徑426mm，壁厚20mm，長13.4m，重43.43kN，密度7850kg/m3，彈性模量2.1×1011Pa。
計算分析時，不考慮拉向地面的斜向鋼索，直接從柱頂點開始向中心鋼管建模。鋼絲繩計算金屬面積530mm2，計算重量5.15kg/m（其中1kg為附加在鋼索上威亞牽引繩的重量）。
1.2 荷載工況
荷載包括：鋼索、中心鋼管、威亞自重，演員、道具重量，溫度荷載等。由于荷載工況組合繁多，本文僅對控制工況進行計算。控制工況分上空索網工況和南北單索工況兩部分，分別見表1、表2。
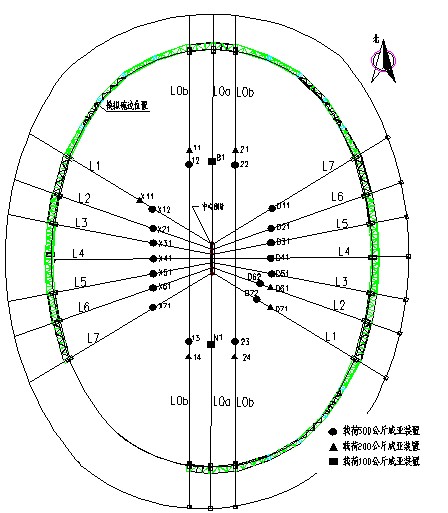
圖1 排練場上空鋼索網及威亞布置圖
表1 上空鋼索網計算工況
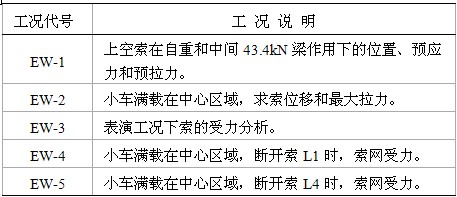
表2 上空南北通長鋼索計算工況
2 索網計算模型
2.1索網找形理論
由于索在無應力情況下沒有剛度，不具有承載力和一定的形狀，所以必須施加適當的預應力來使其產生足夠的剛度并確定形狀。索網結構的形態確定是一個典型的幾何非線性大位移問題，幾何外形的微小變化都會引起結構性能的較大變化。幾何外形、所承受的外荷載和內應力三者之間以非線性方式相互作用和影響。因此，其工作階段的幾何狀態一般是難以在事先確定的，必須通過找形。找形過程的實質就是通過求解在事先確定的邊界條件下建立的非線性方程組，從而獲得與給定的預應力分布相對應的初始幾何形態[1]。在此基礎上，再進行加載和荷載分析。目前，找形分析主要包括力密度法、動力松弛法、基于有限元分析的節點平衡法和支座提升法等[2,3]。
2.1.1 非線性有限元分析
由于索網結構在荷載作用下一般處于小應變、大位移狀態，所以該類結構有限元計算需考慮結構的幾何非線性問題。采用坐標列式U. L (Update Lagrange) 方法，根據虛功原理可得非線性結構在任意時刻t時，結構變形的增量平衡方程為[4,5]：
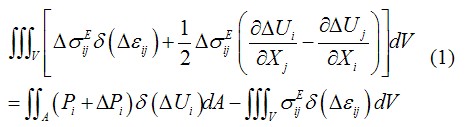
根據最小勢能原理可建立有限元基本方程，其整體坐標系中單元的基本方程為：
為單元的非線性剛度矩陣；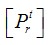 
為節點不平衡力。解這類方程組為加速收斂和減小求解誤差，采用Newton-Raphson方法和增量方法求解較為合適。
2.1.2 力密度法
力密度法是由Linkwitz、Schek[6]等提出的一種用于索網結構的找形方法。其基本原理是：將膜結構離散為節點和桿元組成的索網結構模型，對每一節點建立靜力平衡方程，通過預先給定力密度值，將幾何非線性問題轉化為線性問題，聯立求解一組線性方程組得到索網各節點的坐標。如圖2所示，對索網中任意節點 ，承受集中力 ，與此節點相連接的桿元為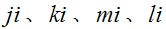
。根據靜力平衡得方程式：
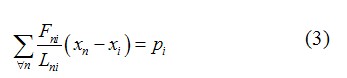
式中：n 為i 點相連的各節點；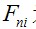 
為與i 節點相鄰的桿元的內力； 
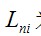為與i 節點相鄰的桿元的長度；
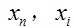為節點坐標列向量； 為荷載列向量。
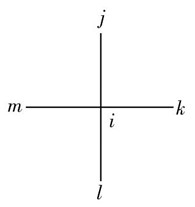
圖2 節點受力模型圖
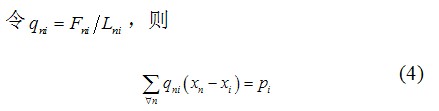
由于力密度法只要求給出離散后結構各桿件的幾何拓撲關系、力密度值和邊界節點坐標，即可建立關于節點坐標的線性方程組，并求得節點的真實坐標，避免了初始坐標錄入問題和非線性收斂問題，因而計算速度快，計算精度也能滿足工程要求。
2.2 索網的找形
索網的找形采用力密度法和基于非線性有限元分析的節點平衡法。分別采用程序ANSYS和德國索膜軟件EASY 8.0實現。由于EASY是專業索膜軟件，索網的找形通過建立模型，輸入參數－找力與結構的平衡關系－梁單元分析即可實現。
ANSYS是一個大型的有限元通用程序，對索網的找形稍微復雜，主要計算步驟如下：先以柱頂點和中心鋼管為控制關鍵點，建立初設形態的模型，劃分單元，指定索的材料參數和初應力。然后施加重力荷載，在支座點約束平動自由度，考慮大變形與應力剛化效應，采用Full Newton Raphson 法計算索網結構的初始形態，得到模型在初設形態和初始預應力條件下的平衡狀態，將計算位移結果采用ANSYS的UPGEOM命令更新結構幾何體型，再進行迭代計算，直到更新體型后計算的位移差值達到毫米級為止，完成找形。由于索網結構工作在彈性階段，因此有限元分析時，不考慮結構材料的非線性，僅考慮幾何非線性的影響。
3 索網受力特點及計算結果分析
3.1 有限元法與力密度法結果的比較
自重下索網的應力和變形ANSYS計算結果見圖3。表演工況下索網的內力和變形EASY計算結果見圖4。
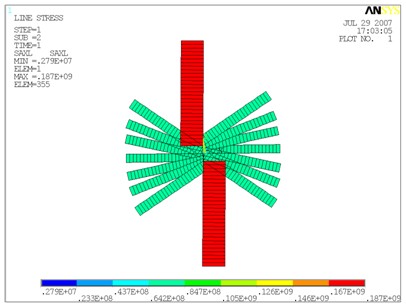
(a) 索網應力圖
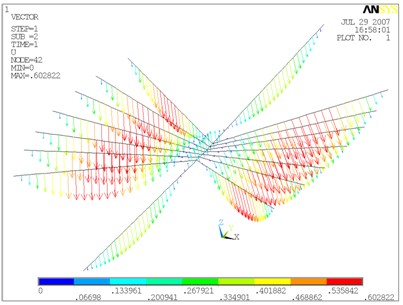
(b)索網相對初始變形
圖3 自重下索網的應力及初始變形
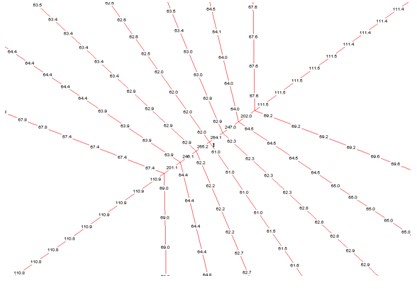
(a) 索網單元及內力分布
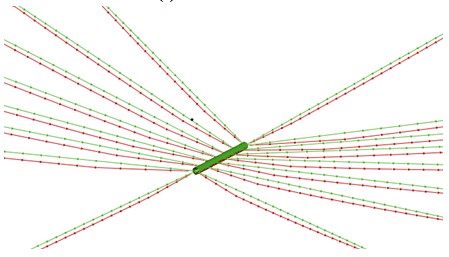
(b)索網變形圖
圖4 表演工況下索網的內力及變形
3和表4分別是自重和表演工況下ANSYS與EASY計算結果比較。
表3 自重下索網ANSYS與EASY結果比較
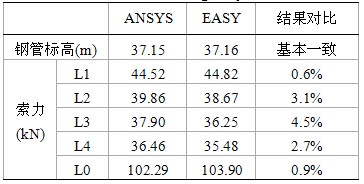
表4 表演工況下ANSYS與EASY結果比較
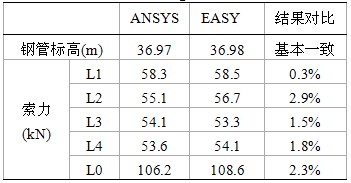
從結果對比可以看出，兩種方法計算的結果基本一致，誤差在5%范圍以內，說明計算結果可信。
3.2 數值解與理論解的比較
南北單索實際上就是一個單跨度的懸索，有理論解。一個集中荷載的單跨度懸索跨中最大撓度計算公式為
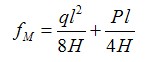（5）
式中： 為懸索線荷載，kg； 為懸索跨度，m；l 為懸索集中荷載，kg；H 為懸索張力，kg；fm 為懸索跨中最大撓度，m。
根據公式（5），得到一個集中荷載的單跨度懸索張力計算公式
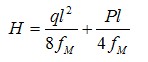（6）
南北單索的工況計算結果見表5。
表5 ANSYS計算索拉力與解析解比較
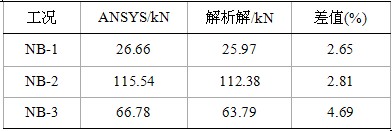
注：單索最小安全系數=最小破斷力/最大內力標準值=5.45
表5表明，ANSYS計算結果與解析解相差在5%之內，說明數值計算結果可信。同時，計算表明，南北單索的最小安全系數為5.45。
3.3 交叉鋼索網計算結果及分析
在上述驗證計算模型的基礎上，不同工況下索網的受力進行了計算分析。計算結果分別見表6和圖5、圖6。
表6 不同工況下索網受力 kN
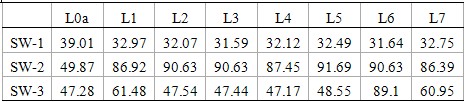
注：①由于索網關于中心180°旋轉對稱，因此只給出了一半索網的受力；②最小安全系數=6.89。
從表6可以看出，無論是在自重還是在極限荷載作用下，索網各根鋼索的內力大小基本一致。說明上空索網的受力均勻，是一個內力分布均勻、自適用能力很強的自平衡體系。斷開一根索后，整個索網的內力重分布（圖5、圖6）特點，更加清楚的說明了這一點：斷開鋼索L1后，鋼索L2內力最大值126.9kN，鋼索L3內力最大值111.4kN，其它鋼索的內力值在80~90kN左右；斷開鋼索L4后，鋼索L2、L3、L5、L6內力最大值在104kN左右，對稱7根鋼索的內力值有所減小，約84kN左右；說明上空交叉索網結構是一個內力分布均勻、內力重新分配調節能力很強的自適用平衡體系。上空索網的最小安全系數為6.89。
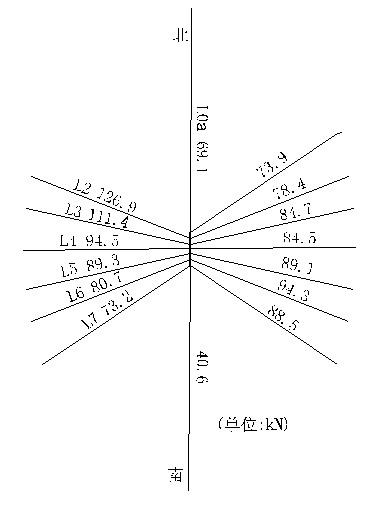
圖5 斷開L1后索網受力
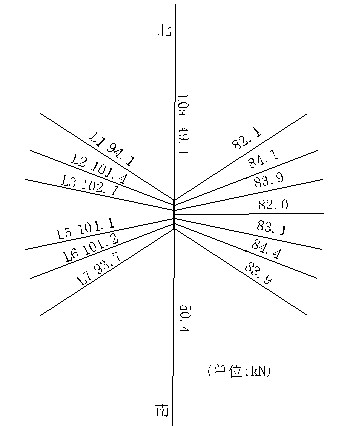
圖6 斷開L4后索網受力
4 結論
采用理論分析和數值計算的方法，利用ANSYS和EASY程序，對奧運會排練場上空鋼索的受力進行了分析。結果表明，
1)兩種方法的數值解和理論解析解結果基本一致，說明數值計算結果真實、可信。
2)南北單索的最大內力值為115.54kN。
3)交叉索網是一個內力重新分配能力很強的自適用體系，最大拉力91.69kN。
4)上空索網結構受力合理，安全可靠。
參考文獻
[1] LI Yang，GAO Ri，YAN Jing-ton. The influence of form-finding for cable net structures by self-weight [J]. Building Science Research of Sichuan，2003，29(2)：29-31 (in Chinese).
[2] XIA Zheng-chun，LI Li，SHI Xiao-wei. Camparison between two methods for form finding of prestressed cable nets [J]. Journal of Wuhan Urban Construction Institute，2005，22(1)：66-69，77 (in Chinese).
[3] ZENG Xiao-fei，YE Ji-hong，YE Ye. Comparisons between dynamic-relaxation method and force-density method for form finding of pretensioned cable roofs [J]. Spatial Structures, 2003, 9(4):55-58 (in Chinese).
[4] Li Renpei. The nonlinear finite element analysis of cable net structures [D]. Chongqing: College of Civil Engineering Chongqing University, 2006.
[5] You Guimo, Yao Qian-feng, Shang Ren-jie,et al. Analysis on bearing behaviors of cable-nets structure with cable edge [J]. Steel Structures，2006，21（3）：72-78 (in Chinese).
[6] Schek H J. The Force Density Method for Form–Finding and Computation of General Network[J].Computer Methods in AppliedM echanics and Engineering，1974，3(2)： 115-134.
（總裝備部工程設計研究總院，北京 100028）
： 